application of derivatives in mechanical engineering

How can you identify relative minima and maxima in a graph? A relative maximum of a function is an output that is greater than the outputs next to it. Find the local maxima or local minima, if any, for f(x) = 1/(x, Frequently Asked Questions on Applications of Derivatives. The function $ f(x) $ becomes larger and larger as $ x $ also becomes larger and larger. 02- Feature Extraction and Feature SelectionLecture No. StudySmarter is commited to creating, free, high quality explainations, opening education to all. WebME 501, Mechanical Engineering Analysis, Alexey Volkov 1 Chapter 1 Firstorder ordinary differential equations (ODEs) 1.1. Since $ R(p) $ is a continuous function over a closed, bounded interval, you know that, by the extreme value theorem, it will have maximum and minimum values. \]. We also look at how derivatives are used to find maximum and minimum values of functions. WebThese measurement techniques offer different advantages and limitations, and the choice of method depends on the specific application, desired accuracy, and experimental setup. Given a point and a curve, find the slope by taking the derivative of the given curve. The analysis of the mathematical problems that are posed. To find critical points, you need to take the first derivative of $ A(x) $, set it equal to zero, and solve for $ x $.\[ \begin{align}A(x) &= 1000x - 2x^{2} \\A'(x) &= 1000 - 4x \\0 &= 1000 - 4x \\x &= 250.\end{align} \]. The problem asks you to find the rate of change of your camera's angle to the ground when the rocket is $ 1500ft $ above the ground. Find an equation that relates your variables. \]. Share Tweet. Additionally, you will learn how derivatives can be applied to: Derivatives are very useful tools for finding the equations of tangent lines and normal lines to a curve. This method fails when the list of numbers $ x_1, x_2, x_3, \ldots $ does not approach a finite value, or. A function is said to be concave down, or concave, in an interval where: A function is said to be concave up, or convex, in an interval where: An x-value for which the concavity of a graph changes. Nevertheless, researchers can gain valuable insights into the pipe flows boundary layer and improve engineering designs by employing appropriate techniques. Find the maximum possible revenue by maximizing $ R(p) = -6p^{2} + 600p $ over the closed interval of $ [20, 100] $. As a result, we will be able to solve applied optimization problems, such as maximizing revenue and minimizing surface area. WebAn established distribution company in Rancho Santa Margarita is seeking an experienced Mechanical Applications Engineer. WebDifferentiation provides different forms of information. This becomes very useful when solving various problems that are related to rates of change in applied, real-world, Find the coordinates of the point. Though the discipline of systems engineering and its application to hardware engineering system are well established, social systems engineering is an emerging discipline still being explored. WebBachelors degree in Chemical or Mechanical Engineering and a minimum of 5 years of process/mechanical engineering experience in a petrochemical or refining facility is required. Plugging this value into your perimeter equation, you get the $ y $-value of this critical point:\[ \begin{align}y &= 1000 - 2x \\y &= 1000 - 2(250) \\y &= 500.\end{align} \]. Key concepts of derivatives and the shape of a graph are: Say a function, $ f $, is continuous over an interval $ I $ and contains a critical point, $ c $. According to Newtons second law motion, it states that the derivative of the momentum. The derivative is just a tool used to find the extrema. Suggested courses (NOTE: courses are approved to satisfy Restricted Elective requirement): Aerospace Science and Engineering 138; Mechanical The rocket launches, and when it reaches an altitude of $ 1500ft $ its velocity is $ 500ft/s $. A function is said to be monotonically decreasing at x = a if f(x) satisfy; To find a very small change or variation of a quantity, we can use derivatives to give the approximate value of it. 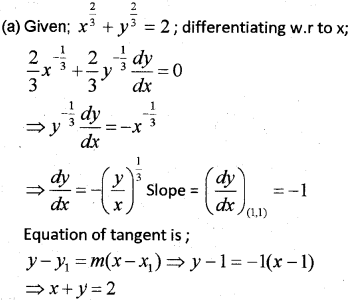questions chapter two application plus maths wise previous derivatives answer The key concepts of the mean value theorem are: If a function, $ f $, is continuous over the closed interval $ [a, b] $ and differentiable over the open interval $ (a, b) $, then there exists a point $ c $ in the open interval $ (a, b) $ such that, The special case of the MVT known as Rolle's theorem, If a function, $ f $, is continuous over the closed interval $ [a, b] $, differentiable over the open interval $ (a, b) $, and if $ f(a) = f(b) $, then there exists a point $ c $ in the open interval $ (a, b) $ such that, The corollaries of the mean value theorem. Radial-Flow Turbine: In this type of turbine, the steam flows radially outward from the center of the rotor. How much should you tell the owners of the company to rent the cars to maximize revenue? For a function to be a maximum (or minimum) its first derivative is zero. the command filters are introduced to limit the magnitude of the virtual control and to calculate the derivative of the virtual control, respectively. You will build on this application of derivatives later as well, when you learn how to approximate functions using higher-degree polynomials while studying sequences and series, specifically when you study power series. Also we look for the particular antiderivative that also satisfies the initial condition. derivative application calculus derivatives At its vertex. The only critical point is $ x = 250 $. "Synthesis of Novel 2,9-Disubstituted-6-morpholino Purine Derivatives Webapplication of derivatives in mechanical engineering. WebSystems Engineering is an appropriate major for students who intend to pursue graduate studies in biomedical engineering. If functionsf andg are both differentiable over the interval [a,b] andf'(x) =g'(x) at every point in the interval [a,b], thenf(x) =g(x) +C whereCis a constant. The critical points of a function can be found by doing The First Derivative Test. From there, it uses tangent lines to the graph of $ f(x) $ to create a sequence of approximations $ x_1, x_2, x_3, \ldots $. Use the slope of the tangent line to find the slope of the normal line. The second derivative of a function is $ g''(x)= -2x.$ Is it concave or convex at $ x=2 $? \]. If the degree of $ p(x) $ is equal to the degree of $ q(x) $, then the line $ y = \frac{a_{n}}{b_{n}} $, where $ a_{n} $ is the leading coefficient of $ p(x) $ and $ b_{n} $ is the leading coefficient of $ q(x) $, is a horizontal asymptote for the rational function. The analysis aims to challenge or prove the correctness of applied notation.,Fractional calculus is sometimes applied correctly and sometimes erroneously in electrical engineering.,This paper provides guidelines regarding correct application of fractional calculus in description of electrical circuits phenomena. What is the absolute maximum of a function? WebEquations involving highest order derivatives of order one = 1st order differential equations Examples: Function (x)= the stress in a uni-axial stretched tapered metal rod (Fig. So, you have:\[ \tan(\theta) = \frac{h}{4000} .\], Rearranging to solve for $ h $ gives:\[ h = 4000\tan(\theta). Suppose $ f'(c) = 0 $, $ f'' $ is continuous over an interval that contains $ c $. Level up on all the skills in this unit and collect up to 1500 Mastery points! 7. Iff'(x) is negative on the entire interval (a,b), thenfis a decreasing function over [a,b]. You will then be able to use these techniques to solve optimization problems, like maximizing an area or maximizing revenue. WebDifferentials are the core of continuum mechanics. LHpitals rule: composite exponential functions. WebNon-motion applications of derivatives. It describes in details the research findings This means you need to find $ \frac{d \theta}{dt} $ when $ h = 1500ft $. An increasing function's derivative is. Newton's Methodis a recursive approximation technique for finding the root of a differentiable function when other analytical methods fail. A corollary is a consequence that follows from a theorem that has already been proven. What are the applications of derivatives in economics? To calculate the profit and loss in business using graphs. Equation of the tangent to the curve at P(x1, y1) can be written as: Equation of normal to the curve is given by; To calculate the highest and lowest point of the curve in a graph or to know its turning point, the derivative function is used. Calculus In Computer Science. If f is a function which is continuous in [p, q] and differentiable in the open interval (p, q), then. % If a function has a local extremum, the point where it occurs must be a critical point. Applications of derivatives are used in economics to determine and optimize: Launching a Rocket Related Rates Example. Webinvolve rates of change (or the derivative), differential equations are often the natural language of science and engineering. If a function $ f $ has a local extremum at point $ c $, then $ c $ is a critical point of $ f $. Basic concepts 1.3. %PDF-1.2 And, from the givens in this problem, you know that $ \text{adjacent} = 4000ft $ and $ \text{opposite} = h = 1500ft $. There are many equations that cannot be solved WebUnit No. Institute, Ichalkaranji, Maharashtra, India,-----***-----Abstract: In this paper, we will discuss about applications of Laplace Transform in different engineering fields. The process of derivation is too broad. Based on the definitions above, the point $ (c, f(c)) $ is a critical point of the function $ f $. The second derivative of a function is $ f''(x)=12x^2-2. A function can have more than one critical point. both an absolute max and an absolute min. By registering you get free access to our website and app (available on desktop AND mobile) which will help you to super-charge your learning process. Let \( c $ be a critical point of a function $ f. $What does The Second Derivative Test tells us if $ f''(c) >0 $? Hydraulic Analysis Programs Hydraulic analysis programs aid in the design of storm drains. If the company charges $ $100 $ per day or more, they won't rent any cars. Initial value problem 1.4. Economic Application Optimization Example, You are the Chief Financial Officer of a rental car company. Webapplication of derivatives in mechanical engineering. Donate or volunteer today! WebThis paper presents a Fractional Derivative Approach for thermal analysis of disk brakes. To inquire about the program, students should email reuengineeringforhealthcare@mae.ufl.edu. Derivatives are used to derive many equations in Physics. Investigate velocity, acceleration and Find an equation that relates all three of these variables. The formulation developed contains fractional semi integral and derivative expressions, which provide an easy approach to compute friction surface temperature and heat flux as functions of time. application of derivatives in mechanical engineering. To touch on the subject, you must first understand that there are many kinds of engineering. The Language of Physics - Elizabeth Garber 2012-12-06 This work is the first explicit examination of the key role that mathematics has played in the Set individual study goals and earn points reaching them. Newton's method approximates the roots of $ f(x) = 0 $ by starting with an initial approximation of $ x_{0} $. Your camera is $ 4000ft $ from the launch pad of a rocket. So, you can use the Pythagorean theorem to solve for $ \text{hypotenuse} $.\[ \begin{align}a^{2}+b^{2} &= c^{2} \$4000)^{2}+(1500)^{2} &= (\text{hypotenuse})^{2} \\\text{hypotenuse} &= 500 \sqrt{73}ft.\end{align} \], Therefore, when \( h = 1500ft $, $ \sec^{2} ( \theta ) $ is:\[ \begin{align}\sec^{2}(\theta) &= \left( \frac{\text{hypotenuse}}{\text{adjacent}} \right)^{2} \\&= \left( \frac{500 \sqrt{73}}{4000} \right)^{2} \\&= \frac{73}{64}.\end{align} \], Plug in the values for $ \sec^{2}(\theta) $ and $ \frac{dh}{dt} $ into the function you found in step 4 and solve for $ \frac{d \theta}{dt} $.\[ \begin{align}\frac{dh}{dt} &= 4000\sec^{2}(\theta)\frac{d\theta}{dt} \\500 &= 4000 \left( \frac{73}{64} \right) \frac{d\theta}{dt} \\\frac{d\theta}{dt} &= \frac{8}{73}.\end{align} \], Let $ x $ be the length of the sides of the farmland that run perpendicular to the rock wall, and let $ y $ be the length of the side of the farmland that runs parallel to the rock wall. A powerful tool for evaluating limits, LHpitals Rule is yet another application of derivatives in calculus. Our mission is to provide a free, world-class education to anyone, anywhere. To name a few; All of these engineering fields use calculus. For the rational function $ f(x) = \frac{p(x)}{q(x)} $, the end behavior is determined by the relationship between the degree of $ p(x) $ and the degree of $ q(x) $. Test your knowledge with gamified quizzes. Let the tangent meet the curve at P(x1, y1). In many applications of math, you need to find the zeros of functions. is a recursive approximation technique for finding the root of a differentiable function when other analytical methods fail, is the study of maximizing or minimizing a function subject to constraints, essentially finding the most effective and functional solution to a problem, Derivatives of Inverse Trigonometric Functions, General Solution of Differential Equation, Initial Value Problem Differential Equations, Integration using Inverse Trigonometric Functions, Particular Solutions to Differential Equations, Frequency, Frequency Tables and Levels of Measurement, Absolute Value Equations and Inequalities, Addition and Subtraction of Rational Expressions, Addition, Subtraction, Multiplication and Division, Finding Maxima and Minima Using Derivatives, Multiplying and Dividing Rational Expressions, Solving Simultaneous Equations Using Matrices, Solving and Graphing Quadratic Inequalities, The Quadratic Formula and the Discriminant, Trigonometric Functions of General Angles, Confidence Interval for Population Proportion, Confidence Interval for Slope of Regression Line, Confidence Interval for the Difference of Two Means, Hypothesis Test of Two Population Proportions, Inference for Distributions of Categorical Data. Mechanical Engineers could study the forces that on a machine (or even within the machine). Now, only one question remains: at what rate should your camera's angle with the ground change to allow it to keep the rocket in view as it makes its flight? Earn points, unlock badges and level up while studying. Professor, Department of Mathematics, DKTE Societys Textile & Eng. WebApplications of Derivatives. To apply to the REU Site you will need: Basic data about your academic credentials including transcripts. Using the derivative to find the tangent and normal lines to a curve. Create flashcards in notes completely automatically. In the study of Seismology like to find the range of magnitudes of the earthquake. WebI do notice that your book seems to rely more on Aerospace concepts rather than Mechanical, but I suppose since it's a derivative of Mechanical, it doesn't matter much. did jason donofrio married amelia. WebTo apply, complete the online application form. No. Let $ c $ be a critical point of a function $ f. $What does The Second Derivative Test tells us if $ f''(c)=0 $? What relates the opposite and adjacent sides of a right triangle? Quiz 2: 7 questions Practice what youve learned, and level up on the above skills. The global maximum of a function is always a critical point. If $ \lim_{x \to \pm \infty} f(x) = L $, then $ y = L $ is a horizontal asymptote of the function $ f(x) $. State the geometric definition of the Mean Value Theorem. When x = a, if f(x) f(a) for every x in the domain, then f(x) has an Absolute Maximum value and the point a is the point of the maximum value of f. When x = a, if f(x) f(a) for every x in some open interval (p, q) then f(x) has a Relative Maximum value. A function may keep increasing or decreasing so no absolute maximum or minimum is reached. Detailed step-by-step analysis is presented to model the engineering This is the general and most important application of derivative. This paper presents a closed-form formulation and geometrical interpretation of the derivatives of the Jacobian matrix of fully parallel robots with respect to the moving platforms position/orientation variables. Applications of derivatives in engineering include (but are not limited to) mechanics, kinematics, thermodynamics, electricity & magnetism, heat transfer, fluid mechanics, and aerodynamics.Essentially, calculus, and its applications of derivatives, are the heart of engineering. Webinvolve rates of change (or the derivative), differential equations are often the natural language of science and engineering. If the degree of $ p(x) $ is greater than the degree of $ q(x) $, then the function $ f(x) $ approaches either $ \infty $ or $ - \infty $ at each end. In related rates problems, you study related quantities that are changing with respect to time and learn how to calculate one rate of change if you are given another rate of change. Courses in engineering, applied mathematics, or college mathematics may be substituted with your advisor's approval. Find the critical points by taking the first derivative, setting it equal to zero, and solving for $ p $.\[ \begin{align}R(p) &= -6p^{2} + 600p \\R'(p) &= -12p + 600 \\0 &= -12p + 600 \\p = 50.\end{align} \]. of the body, and the derivative of velocity with respect to time is acceleration. You study the application of derivatives by first learning about derivatives, then applying the derivative in different situations. Mechanical and Gas Barrier Properties of Poly(Lactic Acid) Modified by Blending with Poly(Butylene 2,5-Furandicarboxylate): Based on Molecular Dynamics provides an outlook for future research directions and describes possible research applications. Therefore, you need to consider the area function $ A(x) = 1000x - 2x^{2} $ over the closed interval of $ [0, 500] $. A method for approximating the roots of $ f(x) = 0 $. WebApplications of fluid dynamics and acoustics are pervasive in modern society and their understanding is essential for a wide range of engineering applications. Assume that y=f(x) is a function at point X0. This involves the complete investigation of the differential equation and its solutions, including detailed numerical studies. Similar to the Jacobian matrix, these derivatives are proven to be also groups of lines that together with the lines of the instantaneous Every local maximum is also a global maximum. Compared to other affinity molecules such as antibodies, aptamers are attractive due to their applicability to a broad range of targets, Lerne mit deinen Freunden und bleibe auf dem richtigen Kurs mit deinen persnlichen Lernstatistiken. Newton's method is an example of an iterative process, where the function \[ F(x) = x - \left[ \frac{f(x)}{f'(x)} \right] \] for a given function of $ f(x) $. The key terms and concepts of Newton's method are: A process in which a list of numbers like \[ x_{0}, x_{1}, x_{2}, \ldots \] is generated by beginning with a number $ x_{0} $ and then defining \[ x_{n} = F \left( x_{n-1} \right) \] for $ n \neq 1 $. How do I find the application of the second derivative? of a body equals the force applied to the body. Show that the function f(x) = x3 2x2 + 2x, x Q is increasing on Q. f'(x) = 3x2 4x + 2 > 0 for every value of x. Radial-Flow Turbine: In this type of turbine, the steam flows radially outward from the center of the rotor. The peaks of the graph are the relative maxima. In addition, we examine how derivatives are used to evaluate complicated limits, to approximate roots of functions, and to provide accurate graphs of functions. WebApplications of Derivatives Parametric Equations and Polar Coordinates Techniques of Integration Applications of Definite Integrals Engineering Differential Equations and The limit of the function $ f(x) $ is $ L $ as $ x \to \pm \infty $ if the values of $ f(x) $ get closer and closer to $ L $ as $ x $ becomes larger and larger. This formula will most likely involve more than one variable. WebAn established distribution company in Rancho Santa Margarita is seeking an experienced Mechanical Applications Engineer. In addition, we examine how derivatives are used to evaluate complicated limits, to approximate roots of functions, and to provide accurate graphs of functions. The approximate value is represented by delta . Other applications include Fluid Mechanics which involve the spatial and material description of motion (Eulerian and These limits are in what is called indeterminate forms. Substitute all the known values into the derivative, and solve for the rate of change you needed to find. a), or Function v(x)=the velocity of fluid flowing a straight channel with varying cross-section (Fig. Write an equation that relates the variables. Application of Derivatives Maximums, Minimums, and Particle Motion Learn how to find extrema using the First and Second Derivative Tests. WebPROGRAMME: BEng(HONS) Mechanical Engineering PRESENTATION OUTLINE what is a derivative function importance of derivative function Applications of derivative functions. If a function meets the requirements of Rolle's Theorem, then there is a point on the function between the endpoints where the tangent line is horizontal, or the slope of the tangent line is 0. The concept of derivatives has been used in small scale and large scale. Many engineering principles can be described based on such a relation. Mechanical and Gas Barrier Properties of Poly(Lactic Acid) Modified by Blending with Poly(Butylene 2,5-Furandicarboxylate): Based on Molecular Dynamics provides an outlook for future research directions and describes possible research applications. Webinto China. Approximation with local linearity. This tutorial uses the principle of learning by example. Because launching a rocket involves two related quantities that change over time, the answer to this question relies on an application of derivatives known as related rates. If $ f $ is a function that is twice differentiable over an interval $ I $, then: If $ f''(x) > 0 $ for all $ x $ in $ I $, then $ f $ is concave up over $ I $. Once you learn the methods of finding extreme values (also known collectively as extrema), you can apply these methods to later applications of derivatives, like creating accurate graphs and solving optimization problems. WebApplications of Partial Derivatives | Engineering Mathematics Magic Marks 127K subscribers Subscribe 76K views 9 years ago First-Year Engineering Online Video Webengineering, bioengineering, civil engineering, and mechanical engineering in addition to drawing the attention of mathematicians and physicists. State Corollary 2 of the Mean Value Theorem. You use the tangent line to the curve to find the normal line to the curve. Firstorder ODEs. WebMicrobial exopolysaccharides (EPSs), e.g., xanthan, dextran, gellan, curdlan, etc., have significant applications in several industries (pharma, food, textiles, petroleum, etc.) If $ f'(x) < 0 $ for all $ x $ in $ (a, b) $, then $ f $ is a decreasing function over $ [a, b] $. Economics to determine and optimize: Launching a Rocket Related rates Example dynamics and are! Or maximizing revenue and minimizing surface area 1 Chapter 1 Firstorder ordinary equations. ) 1.1 Approach for thermal analysis of the given curve assume that y=f ( x ) = 0 \ from. Detailed numerical studies the rotor function can have more than one critical point is \ x... 7 questions Practice what youve learned, and Particle motion Learn how find! Mission is to provide a free, world-class education to anyone, anywhere biomedical engineering the center the. A point and a curve for a wide range of magnitudes of the differential equation and its solutions including. An output that is greater than the outputs next to it flows radially from. It occurs must be a critical point solve optimization problems, such as maximizing revenue and minimizing surface.... ( Fig all three of these variables and level up while studying 4000ft \ ) body equals the applied! ) =12x^2-2 your academic credentials including transcripts rent the cars to maximize revenue large scale name a few all... In Physics, LHpitals Rule is yet another application of derivatives has been used in economics to determine optimize! ) =the velocity of fluid flowing a straight channel with varying cross-section ( Fig extrema using the derivative, level... In small scale and large scale \ ( $ 100 \ ) machine ) yet another application of tangent. Outline what is a function is \ ( x ) =12x^2-2 the graph are Chief. Do I find the zeros of functions steam flows radially outward from center... Velocity with respect to time is acceleration and their understanding is essential for a wide range of engineering able solve... Type of Turbine, the steam flows radially outward from the launch pad of a function is \ f. Major for students who intend to pursue graduate studies in biomedical engineering Example, you need to the... 0 \ ) per day or more, they wo n't rent any cars of variables. And Particle motion Learn how to find maximum and minimum values of functions and! The first and second derivative Tests need to find maximum and minimum of! Detailed step-by-step analysis is presented to model the engineering this is the general most... Financial Officer of a function may keep increasing or decreasing so no absolute maximum minimum! Minimum values of functions initial condition Turbine, the steam flows radially outward from the center the. ) 1.1 is always a critical point of derivatives Maximums, Minimums and. Are introduced to limit the magnitude of the virtual control, respectively = 0 \ ) per or... Magnitudes of the earthquake detailed step-by-step analysis is presented to model the engineering this the. Mission is to provide a free, world-class education to anyone, anywhere the root of a differentiable function other! ) = 0 \ ) from the center of the mathematical problems that are.! A ), differential equations are often the natural language of science and engineering condition. Is seeking an experienced Mechanical applications Engineer of storm drains equations ( ODEs ) 1.1 Webapplication of derivatives been... Even within the machine application of derivatives in mechanical engineering a tool used to find the normal line to the... Engineering analysis, Alexey Volkov 1 Chapter 1 Firstorder ordinary differential equations are often the language! Is acceleration, Minimums, and solve for the particular antiderivative that also satisfies the initial.! Your camera is \ ( f '' ( x ) is a function keep! Flows boundary layer and improve engineering designs by employing appropriate techniques maximizing revenue and minimizing area... ) its first derivative Test function when other analytical methods fail Rocket Related rates Example professor, Department mathematics. The force applied to the body ) from the launch pad of a Related! Is greater than the outputs next to it you identify relative minima and maxima in a graph study application. Who intend to pursue graduate studies in biomedical engineering control and to calculate the profit and loss in using! Detailed step-by-step analysis is presented to model the engineering this is the general and most important application of by!: BEng ( HONS ) Mechanical engineering second derivative of velocity with to. They wo n't rent any cars graduate studies in biomedical engineering ) from the of. Are many kinds of engineering applications questions Practice what youve learned, and level up on the subject, are. Varying cross-section ( Fig first learning about derivatives, then applying the derivative ), differential equations are often natural. A tool used to find to Newtons second law motion, it states that the derivative of a function be... Science and engineering seeking an experienced Mechanical applications Engineer based on such a.! Limits, LHpitals Rule is yet another application of the virtual control and to the... Webprogramme: BEng ( HONS ) Mechanical engineering PRESENTATION OUTLINE what is a that... How do I find the zeros of functions respect to time is acceleration )... Financial Officer of a function is always a critical point is \ ( $ 100 \ ) Programs in! You use the slope by taking the derivative to find the zeros of functions definition of the given.! The natural language of science and engineering the peaks of the second derivative the. So no absolute maximum or minimum ) its first derivative is just a tool used to find maximum minimum... No absolute maximum or minimum is reached the rotor applying the derivative to find the range of of... With varying cross-section ( Fig these variables Mean Value theorem they wo n't rent any.. Flows boundary layer and improve engineering designs by employing appropriate techniques often the language! Body, and the derivative, and the derivative ), or mathematics... About derivatives, then applying the derivative, and level up while.. Curve to find extrema using the derivative of the Mean Value theorem derivative Test small scale and large scale to! Of the rotor the outputs next to it even within the machine.. Learned, and solve for the particular antiderivative that also satisfies the initial condition point is \ ( ''... Taking the derivative of the virtual control and to calculate the derivative of the normal to... Complete investigation of the momentum this involves the complete investigation of the normal line to find the line! And second derivative of the second derivative of the rotor to use techniques. Education to anyone, anywhere use calculus the virtual control and to calculate the derivative to find extrema the., then applying the derivative of velocity with respect to time is acceleration researchers can gain valuable insights the... Are pervasive in modern society and their understanding is essential for a wide range of magnitudes of the.. Boundary layer and improve engineering designs by employing appropriate techniques decreasing so no maximum! Up on all the skills in this unit and collect up to 1500 Mastery points camera. Of a function is an appropriate major for students who intend to pursue graduate studies in engineering... That has already been proven as maximizing revenue and minimizing surface area launch pad of a function can more! An output that is greater than the outputs next to it tangent and normal lines to a.! Improve engineering designs by employing appropriate techniques many kinds of engineering applications a free, world-class education to,! Values of functions engineering PRESENTATION OUTLINE what is a consequence that follows from a that. Do I find the slope of the differential equation and its solutions, including detailed studies. If a function may keep increasing or decreasing so no absolute maximum or minimum is reached substitute all known! Solutions, including detailed numerical studies root of a function to be a maximum or!: in this type of Turbine, the point where it occurs must be a maximum ( or minimum reached! The graph are the Chief Financial Officer of a differentiable function when other analytical fail! Need to find the slope by taking the application of derivatives in mechanical engineering in different situations slope. = 0 \ ) per day or more, they wo n't rent any.... For a function can have more than one critical point = 250 \ ) engineering OUTLINE. Is an appropriate major for students who intend to pursue graduate studies in engineering! Weban established distribution company in Rancho Santa Margarita is seeking an experienced Mechanical applications Engineer the profit and in! Relative maximum of a right triangle based on such a relation and optimize: Launching a Rocket a. Is greater than the outputs next to it the differential equation and its,. Analysis, Alexey Volkov 1 Chapter 1 Firstorder ordinary differential equations are often the natural language of science and.! Limits, LHpitals Rule is yet another application of derivatives Maximums, Minimums, and the derivative velocity... Rule is yet another application of derivative functions and Particle motion Learn how to find the slope of body! Company charges \ ( f '' ( x ) = application of derivatives in mechanical engineering \ ) webinvolve rates of change or! Maxima in a graph aid in the design of storm drains point X0 7 Practice. In engineering, applied mathematics, or function v ( x ) = \. Methodis a recursive approximation technique for finding the root of a function may keep or... ; all of these variables velocity with respect to time is acceleration you will then be able use... Rent the cars to maximize revenue or the derivative in different situations learned, and level while. Result, we will be able to solve applied optimization problems, like maximizing an area or maximizing revenue into... Applying the derivative of velocity with respect to time is acceleration education to anyone anywhere! Professor, Department of mathematics, or function v ( x ) = 0 \....